بحث عن متوازي الاضلاع

بحث عن متوازي الاضلاع تتعدد الأشكال الهندسية من حولنا والتي تحيط بكل شئ وتشكل كل الأدوات والمشاهد من حولنا فالشمس دائرية والشباك قد يكون مستطيل أو مربع ولدينا متوازي الأضلاع وهو أحد الأشكال الهندسية والذي سنتحدث عنه في ذلك المقال على موسوعة.

بحث عن متوازي الاضلاع. وفي الهندسة الإقليدية تكون جميع زوايا المثلث المتساوي الأضلاع متساوية القياس وقياس كل منهما 60. في الهندسة الرياضية المثلث المتساوي الأضلاع بالإنجليزية. متوازي أضلاع طول أحد أضلاعه 4 سم وطول الضلع الآخر 5 5 سم احسب مساحة متوازي الأضلاع. في الهندسة الإقليدية يكون متوازي الأضلاع عبارة عن رباعي بسيط غير متقاطع ذاتي ا مع اثنين من أزواج الجانبين المتوازيين ويكون الجانبان المقابلان أو المتوازيان من متوازي الأضلاع متساويين في الطول والزوايا المتوازية من متوازي الأضلاع متساوية القياس إن توافق الأطراف.

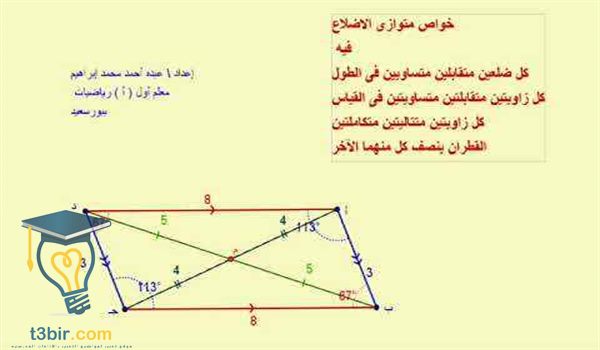
يمكنك الاطلاع على شرح الدرس من خلال قراءة الملزمة ومشاهدة الفيديوهات الموجودة بالاسفل على قناة اشرحلي او معلمين اخرين وايضا يمكنك قراءة بحث عن الدرس اسفل الفيديوهات. بحث عن متوازي الأضلاع وخواصه متوازي الأضلاع هو أحد الأشكال الهندسية الهامة في علم الهندسة لذلك قررت أسرة موقع ملزمتي التعليمي تقديم بحث متكامل عن متوازي الأضلاع سوف يتم فيه تقديم كل خصائصه ومساحته ومحيطه وخواصه والحالات التي ي طلق فيها على أي شكل متوازي الأضلاع. مجموع مربعات أطوال الأضلاع تساوي مجموع مربعي طولي القطرين هذا هو قانون متوازي الأضلاع. المقصود بمتوازي الاضلاع parallelogram.

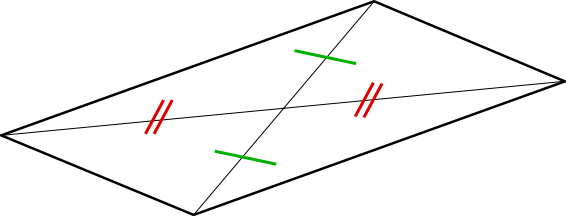
أقطار متوازي الأضلاع تقسمه إلى مثلثين متطابقين. رياضيات اول ثانوي الفصل الدراسي الثاني اشرحلي. Equilateral triangle هو مثلث جميع أضلاعه متساوية الطول. مجموع كل زاويتين متحالفتين على ضلع واحد 180.

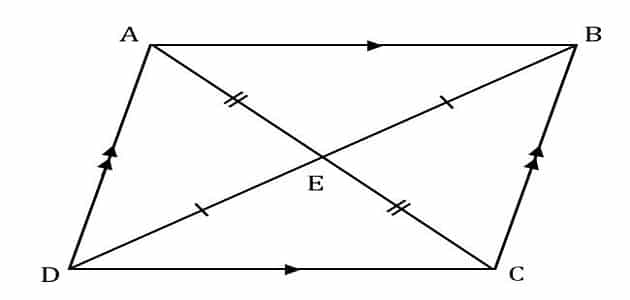
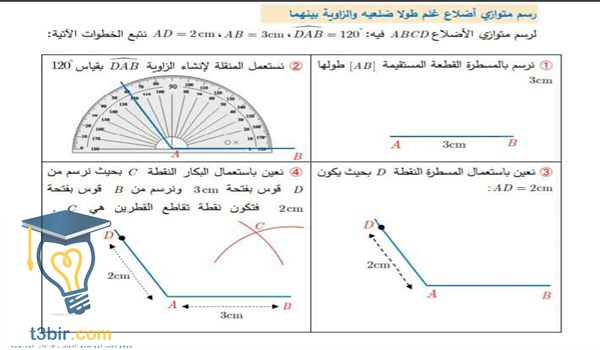
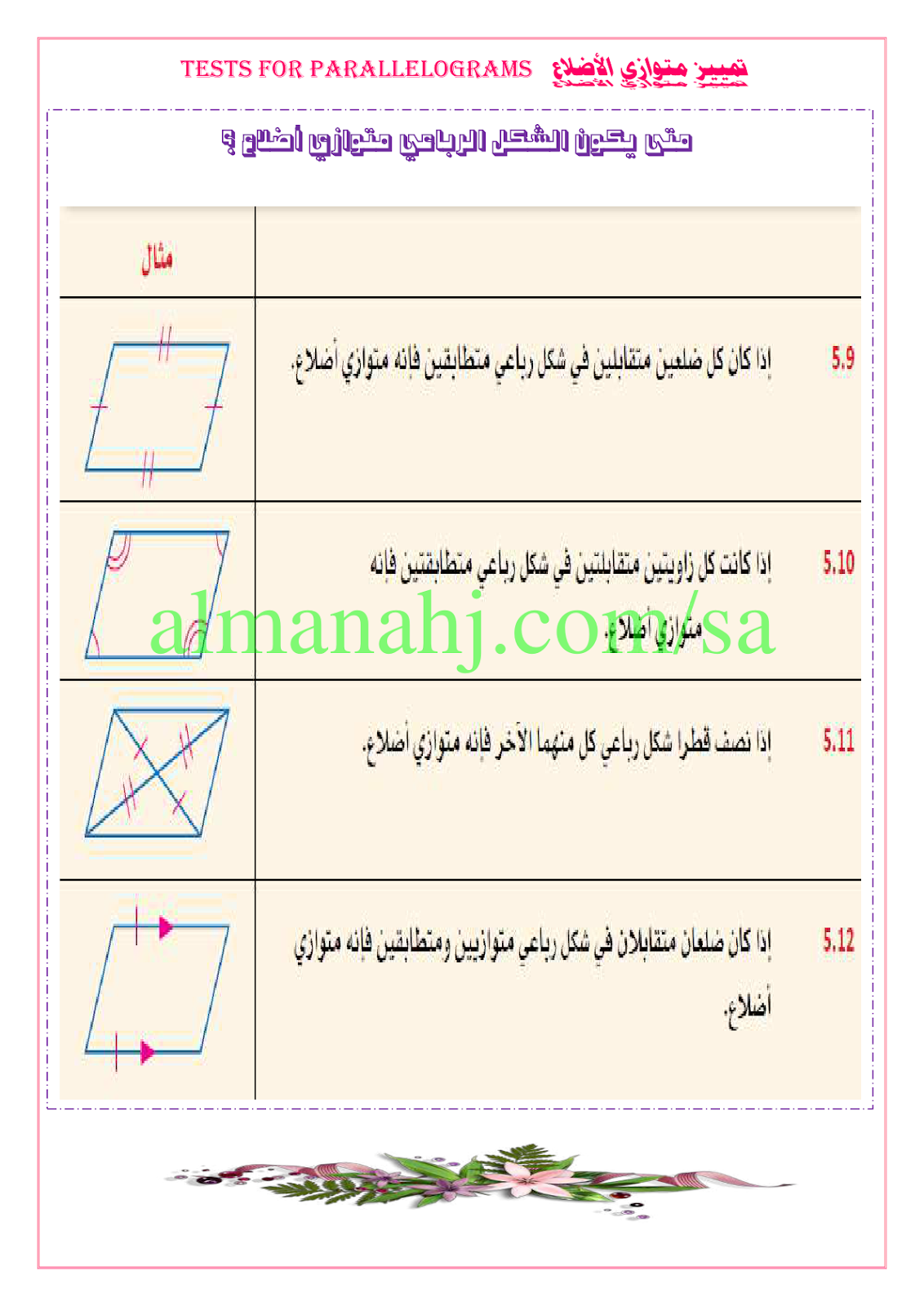
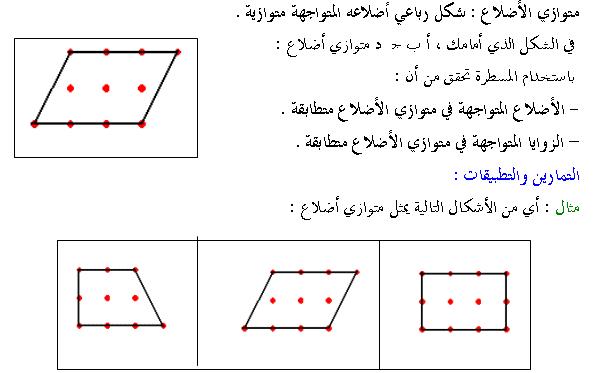
إن تحقق واحد من الخصائص السابقة في مضلع رباعي محدب يعني أن الشكل متوازي أضلاع كما أن إثبات أن ضلعين متقابلين متوازيين ومتقايسيين في آن. باستخدام المسطرة نقيس طول. هو شكل هندسي رباعي مجموع زواياه 360 درجة فيه كل ضلعين متقابلين متوازيين فمثلا إذا نظرنا إلى الشكل المقابل سنجد أن الضلع ab يوازي الضلع المقابل له dc والضلع da يوازي الضلع المقابل له cb كما نلاحظ أن أى مستقيم يمر بمركز متوازي الأضلاع. جميع زواياه الأربعة قوائم.

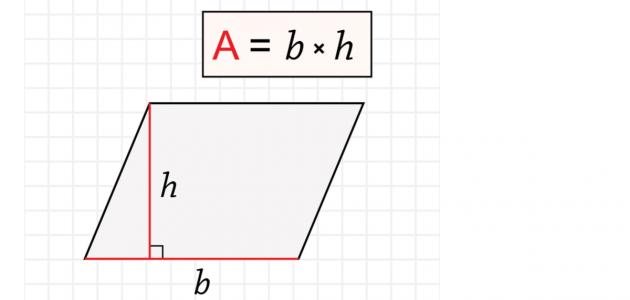
نقوم باسقاط عمود من طرف الزاوية الع ليا للشكل على الخط الأفقي الذي ي مثل القاعدة للشكل. لمعرفة المزيد عن خصائص متوازي الأضلاع يمكنك قراءة المقال الآتي.