بحث عن متباينة المثلث

كما في الشكل.

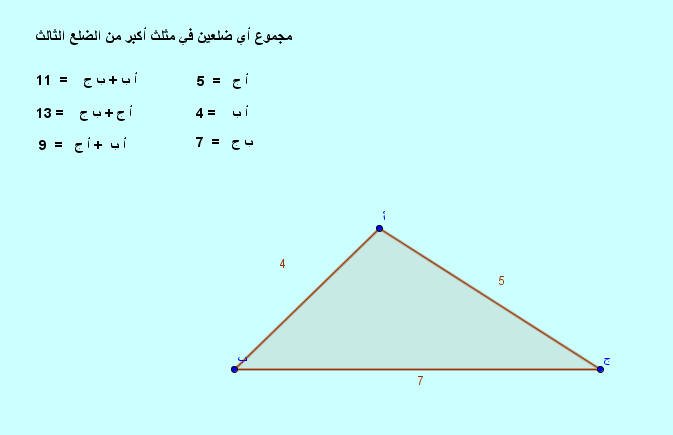
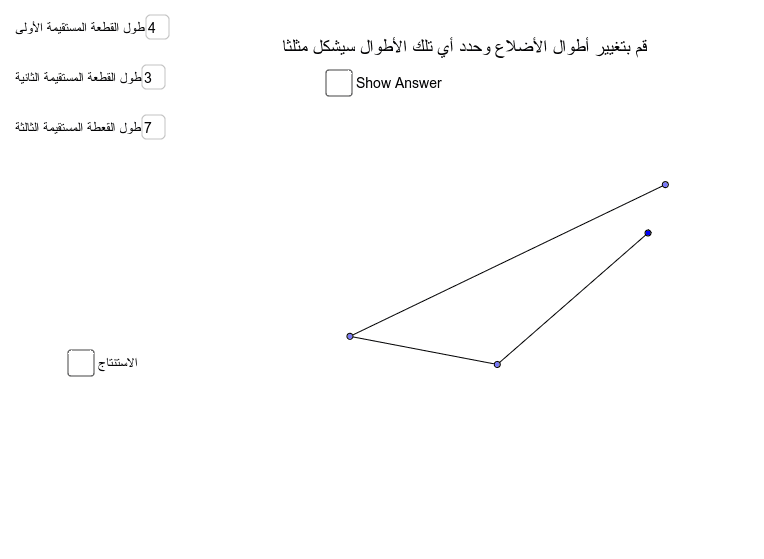
بحث عن متباينة المثلث. مثلث طول ضلعيه هو. ومجموع طولي أي ضلعين في مثلث أكبر من طول الضلع الثالث شرط وجود المثلث. في الواقع أن الأمر ليس كذلك فلو تعمقنا في بحث صفات المثلث سيكشف لنا الواقع عن علاقات مذهلة تلك العلاقات. 3ـأن يميز الطالب بين أطوال الأضلاع التي يمكن اختيارها لتكون مثلث.

2ـ أن يثبت الطالب صحة متباينة المثلث. هذا الأثبات ظهر في كتاب الأصول كتاب1 المقترح 20. عدل سابقا من قبل محمد الباجس في الجمعة أكتوبر 28 2011 6 46 am عدل 2 مرات. لكن ad ab bd ab bc لذلك جمع الضلعين ab bc ac.

لنفرض أن المثلث dbc متساوي الساقين حيث الضلع bc يساوي الضلع bd و ab هو امتداد له. أثبت أقليدس أن الزاوية β α ومنه ad ac. 4ـ أن يجد القيم الممكنة لطول ضلع مجهول إذاعلم طولا الضلعين الآخرين. تسجيل خروج تغيير.

البريد الإلكتروني مطلوب البريد الإلكتروني لن يتم نشره الاسم مطلوب. مع الملاحظة أ ب أ جـ ب جـ في حالة وقوع جـ على القطعة المستقيمة أ ب كما في الشكل. المثلث القائم isosceles triangle with equal sides ab ac divided into two right triangles by an altitude drawn from one of the two base angles. العلاقات بين أقصر الطرق.

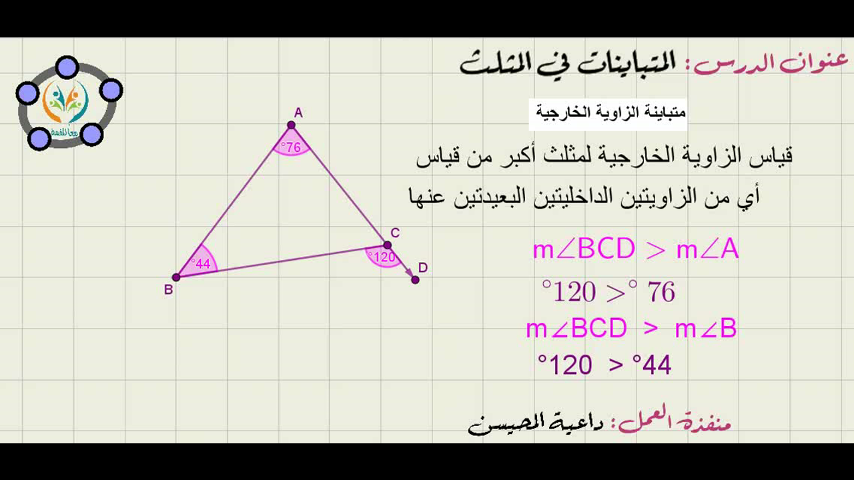
أ 8 7 2 8 7 جتا 33 ومنه أ 4 37 سم. المثلث هو أحد الأشكال الأساسية في الهندسة وهو شكل ثنائي الأبعاد مكون من ثلاثة رؤوس تصل بينها ثلاثة أضلاع وتلك الأضلاع هي قطع مستقيمة. طول أى ضلع فى مثلث أكبر من الفرق بين طولى الضلعين الآخرين وأقل من مجموع طولى الضلعين الآخرين. إملأ الحقول أدناه بالمعلومات المناسبة أو إضغط على إحدى الأيقونات لتسجيل الدخول.

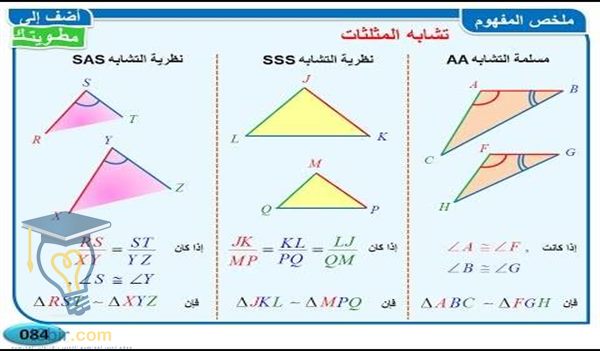
أثبت أقليدس متباينة المثلث من خلال الهندسة الأقليدية من خلال الرسم. الجبر أحد الفروع الرئيسية. متباينة المثلث أو متراجحة المثلث هي المتراجحة التي تنص على أن طول أي ضلع من أضلاع المثلث أصغر حتما من مجموع طول الضلعين الآخرين وأكبر حتما من الفرق بينهما. وانتهت كنظرية تنص على.

ج 7 سم ب 8 سم وقياس الزاوية المقابلة للضلع أ أ 33 ما هو طول الضلع أ وقياس باقي الزوايا. والمثلث الذي رؤوسه هي a و b و c يرمز له بالرمز.