بحث عن زوايا المثلثات

بحث عن زوايا المضلع في الرياضيات إن أي شكل هندسي مغلق مستوى يتكون من أضلاع مستقيمة وله عدد من الزوايا فيطلق عليه اسم مضلع والزاوية يطلق عليها أنها تمثل نقطة التقاء ضلعين أو مستقيمين ويتم تقسيم المضلعات إلى مضلعات منتظمة حيث تكون هناك مضلعات متساوية في اطوال اضلاعها.

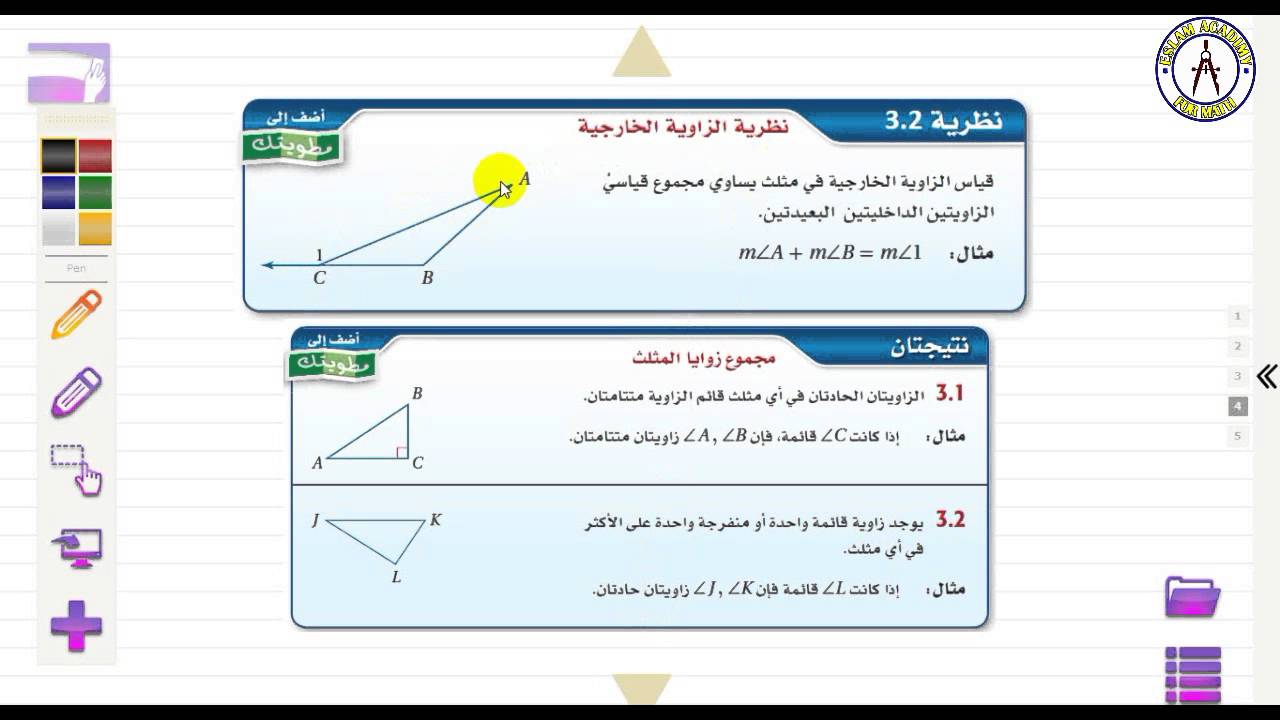
بحث عن زوايا المثلثات. في هذا الدرس سنتعرف على منصفات مثلث بإعتبار أن منصف مثلث هو أحد المستقيمات الهامة في المثلث و تكمن الأهمية في كون أن هذه المستقيمات تحقق خاصية لم يسبق لنا ان تعرفنا عليها بعد. الرأس أ والرأس ب والرأس ج في عرف الم ثلث حينها باسم المثلث أب. يتم استخدام المثلثات في الهندسة المعمارية حيث لا يمكن أن يتم بناء أي منزل أو مبنى دون أن يتم قياس الزوايا الموجودة في جدران المنزل وكذلك قياس الأعمدة حتى يتم الابتعاد على عن أي انهيار منزلي أو تشوهات في الجدران. كما يوحي الاسم فيمكن القول أن تلك الزوايا الثلاث هي عبارة عن مضلع ذو ثلاث زوايا يكون ذلك المضلع مغلقا بطريقة ما وذلك لكي يكون لديه ثلاثة قطاعات أو سطور ذات بداية ونهاية وبالتالي يمكن القول أن المثلث هو مضلع له ثلاثة جوانب وثلاث زوايا وثلاثة رؤوس ومجموع الزوايا.

المثلث هو أحد الأشكال الأساسية في الهندسة وهو شكل ثنائي الأبعاد مكون من ثلاثة رؤوس تصل بينها ثلاثة أضلاع وتلك الأضلاع هي قطع مستقيمة. المثلث يعرف المثلث على انه أحد الاشكال الهندسية الهامة في الرياضيات يوجد به بعض الرسومات المستقيمة والتي تعرف باسم الاضلع تلك الاضلع التي تتكون منها المثلث الذي يصل الى ثلاث نقاط تلك النقاط الهامة التي تعرف باسم الرؤوس وبالتالي يتكون الينا المثلث المغلق. ي عرف الم ثلث على أن ه ش ك ل م غلق يحتوي على ثلاثة خطوط م ستقيمة تلتقي معا في نقاط معي نة ت عرف باسم رؤوس المثلث ويتم تسمية الم ثلث ن سبة إلى أسماء رؤوسه فإذا كانت رؤوس المثلث هي. نظرة عامة حول المثلث.

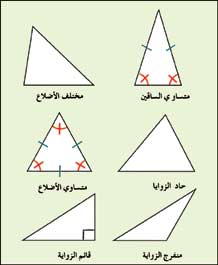
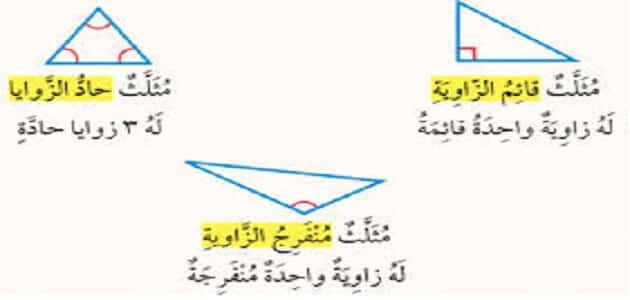
ومجموع طولي أي ضلعين في مثلث أكبر من طول الضلع الثالث شرط وجود المثلث. يمكنك ايضا الاطلاع على مزيد من المعلومات عن زوايا المثلثات وفقا لزواياها من خلال الويكيبيديا زوايا المثلثات وفقا لاضلاعها ويكيبيديا. تصنف المثلثات وفقا لاضلاعها ان كانت متطابقة الاضلاع او متطابقة الضلعين او مختلفة الاضلاع. سنبدأ بإعطاء تعريف لمنصف مثلث ثم بعد ذلك.

بحث رياضيات عن المثلثات كتابة سناء موسى آخر تحديث.