بحث عن الدوال الخاصة

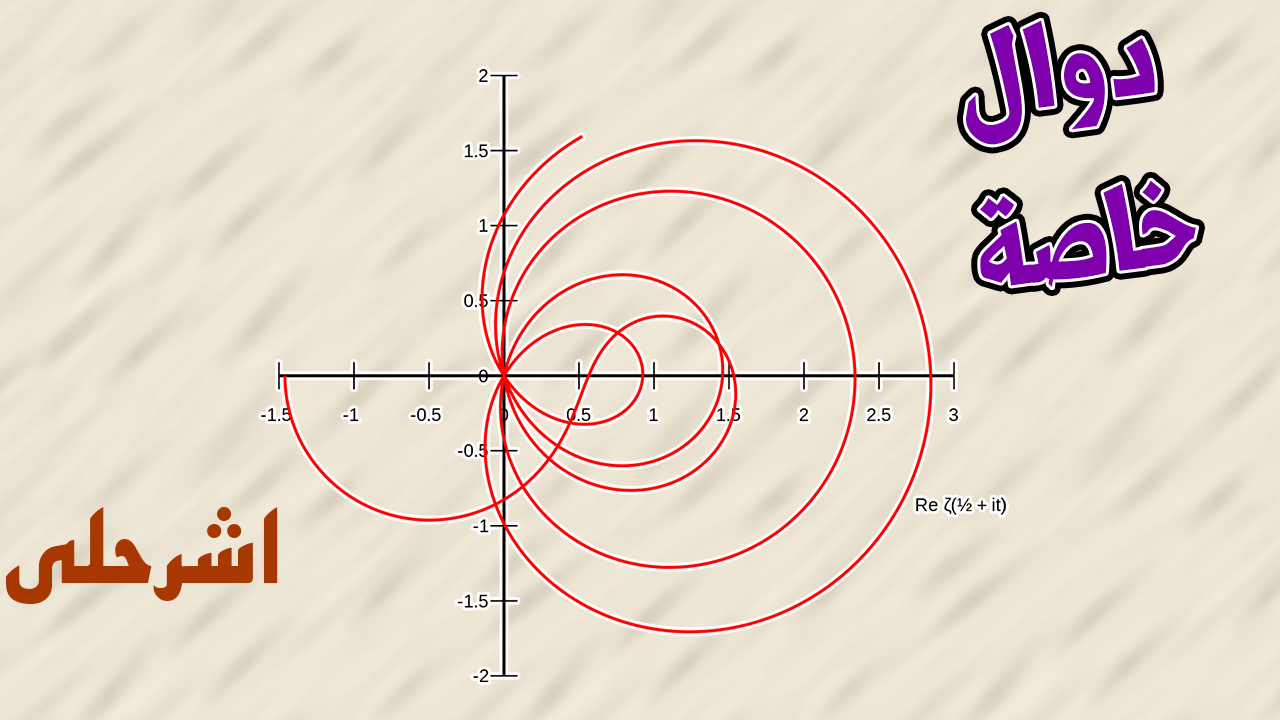
صفحات تصنيف دوال خاصة.

بحث عن الدوال الخاصة. أولا قاعدة الجبر الأولي. غالب ا ما نخصص لفظ دالة للتطبيقات التي يكون مستقرها الدوال العددية أو الدوال العقدية. في حين نسمي تطبيق ا كل ما يحقق التعريف أعلاه. الدوال ذات متغيرين مستقلين مثل.

المجموعة a تدعى مجال التناظر والمجموعة b تدعى مدى التناظر. في هذا الدرس نتعلم بعض بعض الخصائص والمفاهيم المتعلقة بالدوال خاصة. B a العلاقة بين عناصر المجموعة a و بين عناصر المجموعة b تدعى تناظر. وأغلب هذه الدوال تظهر عند حل المعادلات التفاضلية أو للتكاملات.

مثل الدالة الدرجية دالة اكبر عدد صحيح ودالة القيمة المطلقة. بالإضافة إلى ذلك فإن الدوال الخاصة تمتلك من المهارات والآليات الرياضية الفائقة القدرة على التبسيط. يشتمل هذا التصنيف على 25 صفحة من أصل 25. الكثير من الطلبة يجدون صعوبة بالغة في علم الرياضيات ولذلك يسعدنا ان نقدم لكم في مقال اليوم بحث عن الدوال وليس على الطالب إلا الصبر والتركيز كي يتعلم علم الدوال وهذا ليس لصعوبته بل لأنه علم واسع ملئ بالأفكار الكثيرة وفي هذا المقال سنناقش كل ما يتعلق بالدوال الذي.

يمكن تعريف الجبر الأولى على أنه الدراسة المبكرة لعلم الجبر وقد يكون دراسة مبكرة لعلم الرياضيات بشكل عام ويشمل دراسة أهم مبادئ علم الجبر وهم العمليات الحسابية الأربعة والمجموعات العددية والنسب والمعادلات البدائية البسيطة والإشارات. الدوال الخاصة ببساطة هي دوال رياضية معينة لها أهميتها العالية في التحليل الرياضي أو الفيزياء. مثل حجم متوازي المستطيلات. الدوال ذات ثلاثة متغيرات مستقلة.

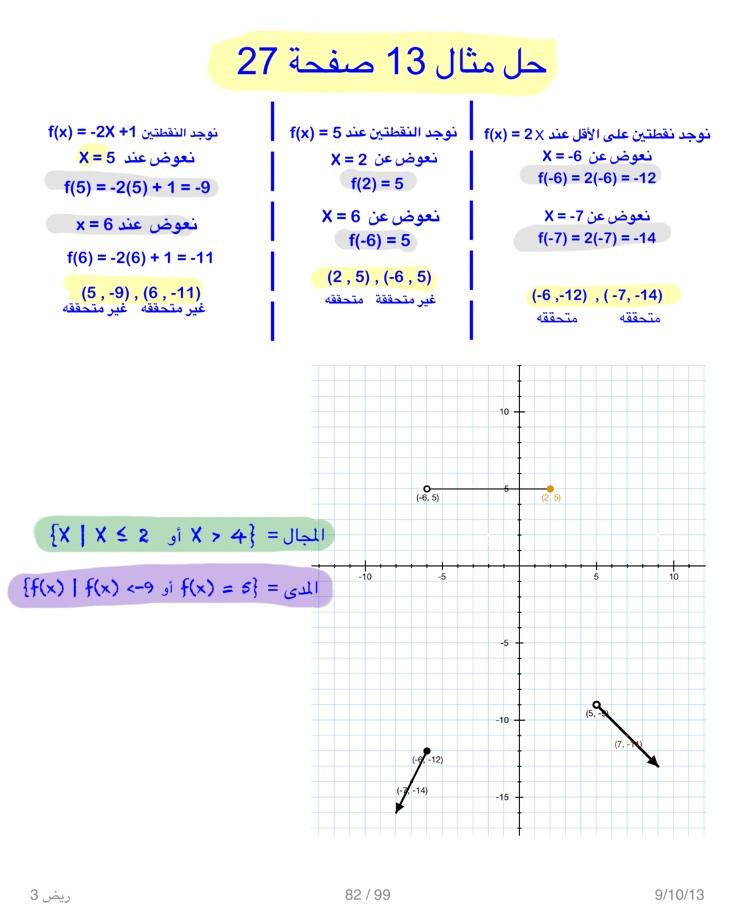
مثل العلاقة بين الدخل والإنفاق. كل عنصر في المجموعة b المدى وله مصدر يدعى صورة. كل عنصر في المجموعة a المجال يدعى مصدر أو أصل. نتعلم ايضا في هذا الدرس عن الدوالة المتعددة التعريف.